

But the most interesting part is how the Fibonacci numbers, the Golden Proportion, and the Golden rectangle are all contained in the Golden spiral. So far this has been about straight proportions. This is a golden rectangle: the ratio of its long to short side is 1.618… That’s because it’s based on an irrational number. It’s a dynamic form–the brain tries, but just can’t quite map out this rectangle using simple numbers. They passed this secret formula down through the centuries to create what is considered the most harmonious relationship between visual elements.

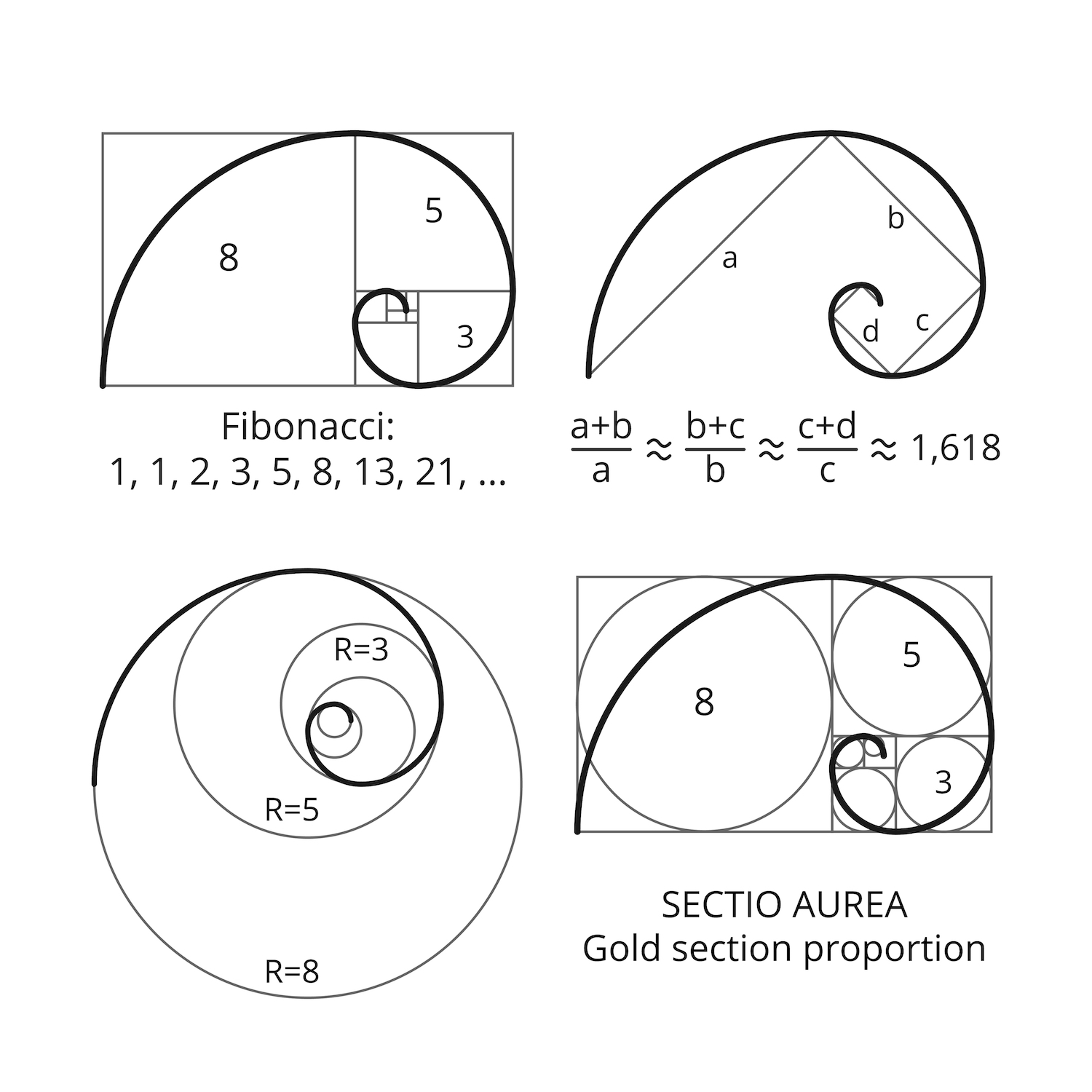
Once they discovered it in nature, artists, philosophers, mathematicians, and architects used this ratio in their work. The proportions of the sides of this rectangle are 1 to 1.618. One reason this ratio is so admired is that it’s found in the golden rectangle. To prove this, I’ll present the following 5 second video clip. This proportion was so admired by architects, artists, and mathematicians throughout history that it was called “golden” even “sacred.” Some call these numbers and their resulting geometries the basis of our perception of beauty. 1.618ġ.618, one of the most famous irrational numbers, is also called the Golden ratio, 1:1.618…. For your glimpse of this slice of infinity, I calculated Phi out to 100,000 places. Because Phi is an irrational number, it goes to infinity, never repeating, getting ever closer to Phi, but never reaching a precise, definable quantity. I put ellipsis after it because the decimals go on to infinity). What mathematicians discovered about the Fibonacci sequence is that the ratios of the successive numbers in the Fibonacci sequence–that is, dividing one number in the sequence by the previous one–getting closer and closer to a special number, 1.618…. Odd fact: The number of petals on a flower is usually a Fibonacci number. As we’ll see, this sequence and the geometry it forms can be found throughout the natural world. How many rabbits will there be in one year? It was his answer to a popular number riddle: suppose a pair of rabbits, male and female, are able to mate and every month their offspring produce a pair of male and female rabbits. These numbers, 34 and 21, are numbers in the Fibonacci series, and their ratio 1.6190476 closely approximates Phi, 1.6180339.Fibonacci’s famous number sequence was simple: to get the next number in the sequence, add the previous two numbers.
#The fibonacci sequence in nature full#
The DNA molecule measures 34 angstroms long by 21 angstroms wide for each full cycle of its double helix spiral. DNA moleculesĮven the microscopic realm is not immune to Fibonacci. When a hawk approaches its prey, its sharpest view is at an angle to their direction of flight - an angle that's the same as the spiral's pitch. And as noted, bee physiology also follows along the Golden Curve rather nicely. Following the same pattern, females have 2, 3, 5, 8, 13, and so on. Thus, when it comes to the family tree, males have 2, 3, 5, and 8 grandparents, great-grandparents, gr-gr-grandparents, and gr-gr-gr-grandparents respectively. Males have one parent (a female), whereas females have two (a female and male). In addition, the family tree of honey bees also follows the familiar pattern. The answer is typically something very close to 1.618. The most profound example is by dividing the number of females in a colony by the number of males (females always outnumber males). Speaking of honey bees, they follow Fibonacci in other interesting ways.


 0 kommentar(er)
0 kommentar(er)
